Coordinate Geometry
Video Courtesy of Kaplan GRE prep.
Coordinate Plane
A coordinate plane is formed by the intersection of a horizontal number line, called the x-axis, and a vertical number line, called the y-axis. The number lines intersect at zero at the point called the origin.
The coordinates of a point A(x, y) give the distance from the axes. The value of x gives the distance from the y-axis and the value of y gives the distance from the x-axis.


Slope of a Line
The slope of a line, m, is its slant. The slope can be used to give the rate of change.
The steeper the line, the faster the rate of change.
The formula to find the slope of the line between two points (x1, y1) and (x2, y2) is
slope = m = \dfrac{\,rise\,}{run} = \dfrac{change\,\, in\,\, \textit{y}}{change\,\, in\,\, \textit{x}}
= \dfrac{{\textit{y}}_{\displaystyle{2}} \,-\, \textit{y}_{\displaystyle{1}}}{\textit{x}_{\displaystyle{2}} \,-\, \textit{x}_{\displaystyle{1}}}


The slope of a line can be:
positive


x and y both increase
negative


x and y both decrease
zero


horizontal:
y does not change
undefined


vertical:
x does not change
Example
What is the slope of this line?
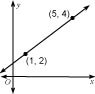

Solution
To solve this problem, plug the digits of the points into the slope formula.
Use (5, 4) as (x2, y2) and (1, 2) as (x1, y1).
m = \dfrac{{\textit{y}}_{\displaystyle{2}} \,-\, \textit{y}_{\displaystyle{1}}}{\textit{x}_{\displaystyle{2}} \,-\, \textit{x}_{\displaystyle{1}}} = \dfrac{4 \,-\, 2}{5\,-\, 1} = \dfrac{2}{4} = \dfrac{1}{2}
The slope of the line is 1/2.
Example
An elm tree grew from 13 feet tall to 26 feet tall in 5 years. An oak tree grew from 8 feet tall to 11 feet tall in 18 months. Which type of tree grew faster?
Solution
This problem is comparing rates of change. The rates must use the same units.
slope = m = \dfrac{change\,\, in\,\, \textit{y}}{change\,\, in\,\, \textit{x}}
= \dfrac{change\,\, in\,\, height \,(feet)}{change\,\, in\,\, time (years)}
elm = m = \dfrac{26 \,-\, 13}{5} = \dfrac{13}{5} = 2.6
oak = m = \dfrac{11 \,-\, 8}{18 \,\,months}
= \dfrac{3}{1.5\,\,years} = 2
The elm tree grows at 2.6 ft/year and the oak grows at 2 ft/year. The elm tree grows faster.
Alternate Method
The question is not asking for the rates, just a comparison of the rates.
Make a quick sketch. Plot the points and compare the lines.
Use points (years, height).
elm = (0, 13) and (5, 26)
oak = (0, 8) and (1.5, 11)


The line showing the rate of change for the elm tree is steeper than the line for the oak tree, so the elm grows faster.
Graphing a Line
A graph of the equation Ax + By = C is a line.
examples:
5x + 2y = 10
2x – y = 7
x = -3
Slope-intercept form
There are two ways to graph a line. One way is to rewrite the equation of the line into slope-intercept form. The slope lets you compare rates of change and find other points on the line.
Solve the equation of the line for y.
y = mx + b where m is the slope and the point (0, b) is the y-intercept where the line crosses the y-axis.


Example
Graph the equation 3x – y = 2.
Solution
Solve the equation 3x – y = 2 for y.
3x – y = 2
3x = y + 2
y = 3x – 2
So the slope is m = 3 and the y-intercept is b = -2.
Plot the point (0, -2).


slope = m = \dfrac{rise}{run} = 3 = \dfrac{3}{1} = \dfrac{up \,\,3}{right\,\, 1}
From point (0, -2), count up 3 and 1 to the right, to the point (1, 1). You can check by counting once more. The point (4, 2) is also on this line.
Graphing intercepts
Another way to graph a line is using the intercepts.
The y-intercept is when x = 0,
the point (0, y).
The x-intercept is when y = 0,
the point (x, 0).
Example
Graph the equation
169x + 65y = 130.
Solution
A quick look at the slope, -169/65, shows the slope-intercept form will be a hard equation to use to graph the equation. Use substitution.
Substitute x = 0 into the equation.
0 + 65y = 130,
so y = 2 (0, 2)
Substitute y = 0 into the equation.
169x + 65(0) = 130
13(13x) = 13(10) 13x = 10
so x = 10/13. (10/13, 0)
Plot the two points and graph the line.


Writing the Equation of a Line
An equation of a line can be found from two points, or from one point and the slope. Having the equation makes it easier to find other points on the line with specific values, and to make comparisons and predictions for linear data.
For the point (x1, y1) and the slope m, the point-slope formula is
y – y1 = m(x – x1).
To write an equation from two points (x1, y1) and (x2, y2), first find the slope of the line.
slope = m = \dfrac{{\textit{y}}_{\displaystyle{2}} \,-\, \textit{y}_{\displaystyle{1}}}{\textit{x}_{\displaystyle{2}} \,-\, \textit{x}_{\displaystyle{1}}}
Then substitute the slope m and one of the points into the point-slope formula.
Example
Write the equation of the line that passes through (1, 3) and has the slope -5.
Solution
Substitute into the point-slope formula.
y – 3 = -5(x – 1)
y – 3 = -5x + 5
y = -5x + 8
Example
Write the equation of the line that passes through (2, 7) and (-2, -1).
Solution
Find the slope.
m = \dfrac{7 \,-\, (-1)}{2 \,-\, (-2)} = \dfrac{8}{4} = 2
The equation has slope 2.
Use the point-slope formula. Since both values are positive, use the point (2, 7).
y – 7 = 2(x – 2)
y – 7 = 2x – 4
y = 2x + 3
The Distance Between Two Points
The distance between two points can be found using the Pythagorean theorem.
(horizontal distance )2
+ (vertical distance )2 = (distance)2
For some points, you can count the distance, such as the points (-2, 1)
and (4, 4).
The horizontal distance is the change in x from (-2, 1) to (4, 4). From -2 to 4 is 6.
The vertical distance is the change in y from (-2, 1) to (4, 4). From 1 to 4 is 3.


So the distance between the points is
d2 = 62 + 32
d2 = 36 + 9 = 45
d = \sqrt{45} = \sqrt{9 × 5} = 3\sqrt{5} ≈ 6.7


The formula for the distance between two points (x1, y1) and (x2, y2) is
d = \sqrt{(\textit{x}_{\displaystyle{2}} \,-\, \textit{x}_{\displaystyle{1}})^{\displaystyle{2}} + (\textit{y}_{\displaystyle{2}} \,-\, \textit{y}_{\displaystyle{1}})^{\displaystyle{2}}}
Example
The points (6, 8) and (2, 4) are the endpoints of a diagonal of a square. What is the area of the square?
Solution
Make a sketch.


The horizontal distance and the vertical distance from (2, 4) and (6, 8) are each the length of one side of the square.
The horizontal distance from (2, 4) and (6, 8) is from 2 to 6,
so is 4. s = 4.
Checking, the vertical distance from (2, 4) and (6, 8) is from 4 to 8 so is 4. Again, s = 4.
A = s2 = 42 = 16
The area of the square is 16 square units.
Example
The points A(1, 1), B(4, 5) and
C(8, 1) form a triangle. Find the perimeter and area of triangle ABC.
Solution
Make a sketch.

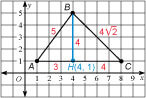
You could use the distance formula to find the side lengths, but remember that the GRE is looking for reasoning, not long calculations. There must be a trick.
Calculate the area first. Draw the height.
The height goes from the point (4, 5) to the side between (1, 1) and (8, 1). The height intersects base AC at the point H(4, 1), and the height h = 4.
The base AC is 7 and the height is 4, so
A = (1/2)(7)(4) = 14
The area is 14 square units.
Look at the right triangles formed with the height.
Triangle AHB is a 3 : 4 : 5 right triangle, so the length of AB is 5.
Triangle CHB is a 45° : 45° : 90° triangle. The side length is 4, so the hypotenuse BC = 4\sqrt{2}.
The perimeter is AB + BC + AC = 5 + 4\sqrt{2} + 7 = 12 + 4\sqrt{2}
Transformations
(Advanced Topic)
There are 3 common transformations that move or change a figure on the coordinate plane.
A translation moves a point or figure some distance up or down, left or right.
Point (x, y) translates to point (x + a, y + b).
A reflection acts like a mirror over a line of reflection. The line of reflection is often an axis, so that point (x, y) reflects to (-x, y) or (x, -y).
A dilation makes a similar figure that is bigger or smaller. It multiplies coordinates by a scale factor. Point (x, y) with scale factor k dilates to point (kx, ky).
Example
The points A(1, 1), B(4, 4) and
C(5, 2) form a triangle. Triangle DEF is the image after translating triangle ABC down 1 and 2 to the right. What are the coordinates of triangle DEF?
Solution
Make a sketch.
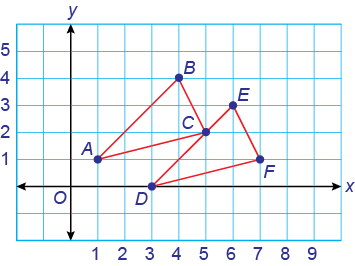
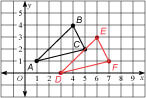
Moving down 1 subtracts 1 from the y-coordinate.
y goes to y – 1
Moving 2 to the right adds 2 to the x-coordinate.
x goes to x + 2
The translation is (x, y) goes to point (x + 2, y – 1).
A(1, 1) → D(3, 0)
B(4, 4) → E(6, 3)
C(5, 2) → F(7, 1)
Example
The points A(2, 1), B(2, 4) and
C(-1, 2) form a triangle.(a) Triangle JKL is the image after reflecting triangle ABC over the x-axis. What are the coordinates of triangle JKL?
(b) Triangle PQR is the image after reflecting triangle ABC over the y-axis. What are the coordinates of triangle PQR?
Solution
Make a sketch.


a) Reflecting over the x-axis changes the value of the y-coordinate: y goes to –y
A(2, 1) → J(2, -1)
B(2, 4) → K(2, -4)
C(-1, 2) → L(-1, -2)
b) Reflecting over the y-axis changes the value of the x-coordinate: x goes to –x
A(2, 1) → P(-2, 1)
B(2, 4) → Q(-2, 4)
C(-1, 2) → R(1, 2)
Example
The points A(3, 0), B(3, 3) and
C(4, 2) form a triangle.(a) Triangle STU is the image of triangle ABC after a dilation with scale factor 2. What are the coordinates of triangle STU?
(b) Triangle VWX is the image of triangle STU after a dilation with scale factor 1/3. What are the coordinates of triangle VWX?
Solution
Make a sketch.


a) A scale factor of 2 multiplies each coordinate by 2.
A(3, 0) → S(6, 0)
B(3, 3) → T(6, 6)
C(4, 2) → U(8, 4)
b) A scale factor of 1/3 multiplies each coordinate by 1/3.
S(6, 0) → V(2, 0)
T(6, 6) → W(2, 2)
U(8, 4) → X(8/3, 4/3)
Before attempting these problems, be sure to review this section on Quantitative Comparison questions.
https://www.youtube.com/watch?v=e2334T1C6Pk&list=PLD0D070C218D8F5A3&index=56
https://www.youtube.com/watch?v=16-Mz70cWF8&list=PLD0D070C218D8F5A3&index=57
https://www.youtube.com/watch?v=dXmAgfjdYxw&list=PLD0D070C218D8F5A3&index=58
https://www.youtube.com/watch?v=OpTasvm6mEQ&list=PLD0D070C218D8F5A3&index=59






