A fraction is a number of the form ±\dfrac{\textit{a}}{\textit{b}}, where a and b are positive integers. The number a is called the numerator and b is called the denominator. The numerator tells you the number of equal parts, and the denominator tells you how many of those parts make up a whole. Often fractions are numbers that fall between integers. Fractions are also used to show division.
Equivalent Fractions
A fraction that has a common factor in both the numerator and denominator is equal to the fraction with the common factor canceled.
\dfrac{6}{10} = \dfrac{3}{5}
(factor 2 in numerator and denominator of \dfrac{6}{10})
Multiplying the numerator and denominator of a fraction by the same (non-zero) number also gives a new fraction which is equivalent to the original fraction.
\dfrac{3}{5} = \dfrac{6}{10} = \dfrac{9}{15} = \dfrac{12}{20}
\\[2ex]\dfrac{3 × 2}{5 × 2} = \dfrac{\,6\,}{10} = \dfrac{6 × 2}{10 × 2} = \dfrac{\,12\,}{20}
-
- If a fraction’s numerator and denominator are equal (e.g. \dfrac{5}{5}), the fraction is equal to 1.
(All 5 pieces of a cake that is cut into 5 pieces is 1 whole cake.)
- If a fraction’s numerator and denominator are equal (e.g. \dfrac{5}{5}), the fraction is equal to 1.
-
- A fraction that has zero as its numerator (e.g. \dfrac{0}{5}) is equal to zero. (Zero pieces of the cake that is cut into 5 pieces.)<br>
-
- A fraction that has zero as its denominator (e.g. \dfrac{8}{0}) is undefined. It isn’t an integer or a rational number.<br>
Simplifying Fractions
To simplify fractions, one method is to use the GCF (greatest common factor)
Divide the numerator and denominator by the GCF to reduce the fraction.
Always reduce fractions to the simplest terms.
The GRE always puts fractions in the lowest possible terms, so you should reduce any fractions to the simplest terms before going to the answer choices. If the GRE answers weren’t in simplest form, there could be confusion about the right answer because there could be two answer choices that were equivalent (e.g., \dfrac{1}{2} and \dfrac{2}{4}).
A fraction with a negative numerator or denominator is equivalent to a negative fraction.
\\[2ex]-\dfrac{\,3\,}{5} = \dfrac{\,-3\,}{5} = \dfrac{\,3\,}{-5}
If both numerator and denominator are negative, the fraction is positive.
\\[2ex]\dfrac{\,-3\,}{-5} = \dfrac{\,3\,}{5}
Example
Reduce \dfrac{275}{525} to lowest possible terms.
Solution
Look for the GCF.
\dfrac{275}{525} = \dfrac{11×25}{21×25} = \dfrac{11}{21}Example
Express \dfrac{26}{16} as a mixed number in lowest terms.
Solution
Find the integer, then simplify the fraction.
\dfrac{26}{16} = 1\dfrac{\,10\,}{16} = 1\dfrac{\,5\,}{8}Another method is to find the prime factors and cancel. This is discuss in the prior chapter.
Example
Reduce \dfrac{220}{594} to simplest terms.
Solution
Do the prime factorization of the numerator and denominator. Cancel the common factors.
\dfrac{220}{594} = \dfrac{2×2×5×11}{2×3×3×3×11}
= \dfrac{2×5}{3×3×3} = \dfrac{10}{27}
Mixed Numbers
Mixed numbers are numbers that are an integer plus a proper fraction.
The number 4\dfrac{\,2\,}{3} is the integer 4, plus the fraction \dfrac{\,2\,}{3}
Any mixed number can be written as a fraction, and any fraction greater than 1 can be written as a mixed number.
Example
Convert 4\dfrac{\,2\,}{3} into an improper fraction.
Solution
One whole is \dfrac{\,3\,}{3},
so 4 wholes = 4 × \dfrac{\,3\,}{3} = \dfrac{\,12\,}{3}
Then add the fractions.
4\dfrac{\,2\,}{3} = \dfrac{\,12\,}{3} + \dfrac{\,2\,}{3} = \dfrac{\,14\,}{3}
To convert an improper fraction to a mixed number, divide the numerator by the denominator. The remainder will be the numerator of the fraction.
Example
Convert \dfrac{79}{9} into a mixed number.
Solution
Divide the numerator by the denominator.
79 ÷ 9 = (8 × 9) + 7
The integer is 8, and the numerator of the fraction is the remainder, 7.
\\[1ex]\dfrac{79}{9} = 8\dfrac{\,7\,}{9}
Multiplying Fractions
How to multiply fractions:
-
-
-
- Cancel out any common factors that appear in numerators and denominators.
- Multiply all numerators to form one numerator and all denominators to form one denominato
-
-
Remember: you DON’T need a common denominator to multiply fractions!
Example
Multiply: \Big(\dfrac{6}{35}\Big)\Big(\dfrac{5}{18}\Big)
Solution
Factor the numerators and denominators. Cancel the common factors.
\Big(\,\dfrac{6}{35}\,\Big) \Big(\,\dfrac{5}{18}\,\Big) = \dfrac{6 × 5}{7 × 5 × 3 × 6}
= \dfrac{1}{7 × 3} = \dfrac{1}{21}
Example
Multiply: \Big(\dfrac{5\textit{x}^{\displaystyle{2}}}{6}\Big) \Big(\dfrac{9}{2\textit{x}}\Big)
Solution
Factor the numerators and denominators. Cancel the common factors.
\Big(\dfrac{5\textit{x}^{\displaystyle{2}}}{6}\Big) \Big(\dfrac{9}{2\textit{x}}\Big) = \dfrac{5 × \textit{x} × \textit{x} × 3 × 3}{2 × 3 × 2 × \textit{x}}
= \dfrac{15\textit{x}}{4}
To multiply mixed numbers, first change the numbers to improper fractions.
Example
Multiply: 3\dfrac{\,1\,}{2} × \dfrac{\,4\,}{5}
Solution
Change 3\dfrac{\,1\,}{2} to an improper fraction. Multiply, then cancel the common factors.
3\dfrac{\,1\,}{2} × \dfrac{\,4\,}{5} = \dfrac{\,7\,}{2} × \dfrac{\,4\,}{5} = \dfrac{7 × 2 × 2}{2 × 5}
= \dfrac{14}{5} = 2\dfrac{\,4\,}{5}
Dividing Fractions
To divide fractions:
-
- change the divisor to its reciprocal, then multiply the fractions. (Remember that the divisor is the second number.)
- The reciprocal of \dfrac{2}{3} is \dfrac{3}{2}. The reciprocal of \dfrac{5}{4} is \dfrac{4}{5}.
- When multiplying, cancel out any common factors that appear in both numerators and denominators.
Example
Divide: \dfrac{(\dfrac{\,5\,}{6})}{(\dfrac{\,7\,}{2})}
Solution
Use the reciprocal. Multiply and cancel the common factors.
\dfrac{\dfrac{\,5\,}{6}}{\dfrac{\,7\,}{2}} = \dfrac{\,5\,}{6} × \dfrac{\,2\,}{7} = \dfrac{\,5\,}{21}To divide mixed numbers, first change the numbers to improper fractions.
Example
Divide: \dfrac{\dfrac{3}{5}}{2\dfrac{1}{10}}
Solution
Change 2\dfrac{1}{10} to an improper fraction. Multiply by the reciprocal, then cancel the common factors.
\dfrac{\dfrac{3}{5}}{2\dfrac{1}{10}} = \dfrac{\dfrac{3}{5}}{\dfrac{21}{10}} = \dfrac{3}{5} × \dfrac{10}{21}
= \dfrac{3 × 2 × 5}{5 × 3 × 7} = \dfrac{2}{7}
Adding and Subtracting Fractions
- To add or subtract fractions that have the same denominator, add or subtract the numerators. Check to see that the answer is in simplest terms.
For example, \dfrac{3}{8}\,-\,\dfrac{1}{8} = \dfrac{2}{8} = \dfrac{1}{4}. - To add or subtract fractions that have different denominators, the first step is to write equivalent fractions that have the same, or a common, denominator.
- To write all fractions with the same denominator, a quick choice is to multiply the denominators. For example,
\dfrac{1}{3} + \dfrac{1}{4} = \dfrac{4}{12} + \dfrac{3}{12} = \dfrac{7}{12}. - But multiplying the denominators may give a rather large denominator. To avoid a large denominator, use the least common denominator (LCD). The LCD is the least common multiple (LCM) of all the denominators.
When adding and subtracting fractions you can split up the numerator, but you can never split up the denominator.
\dfrac{7 + 14}{7} = \dfrac{7}{7} + \dfrac{14}{7} = 1 + 2 = 3
Splitting the numerator works gives you the same value.
\dfrac{7}{7 + 14} ≠ \dfrac{7}{7} + \dfrac{7}{14} = 1 + \dfrac{1}{2}
Splitting the denominator gives you a different value, and is therefore incorrect.
Subtract: \dfrac{7}{12} \,-\, \dfrac{1}{16}
Solution
Find the LCD. Factor the denominators.
12 = 2 × 2 × 3
16 = 2 × 2 × 2 × 2
LCD = (2 × 2 × 3) × (2 × 2) = 48
Find equivalent fractions that have 48 as the denominator.
\\[2ex]\dfrac{7}{12} × \dfrac{4}{4} = \dfrac{28}{48} \dfrac{1}{16} × \dfrac{3}{3} = \dfrac{3}{48}
Subtract. \dfrac{28}{48} \,-\, \dfrac{3}{48} = \dfrac{25}{48}
Video Quiz
Fractions
Best viewed in landscape mode
3 questions with video explanations
100 seconds per question
Are you sure you want to refresh the question?
a https://www.youtube.com/watch?v=Bfiw3E8Gic0
a https://www.youtube.com/watch?v=Jb2FXGCWpX4
a https://www.youtube.com/watch?v=Q47hKZo54nU
a https://www.youtube.com/watch?v=Hn0O6nhiKtE
Complex Fractions
A complex fraction is a fraction that has a fraction in the numerator and/or denominator. In other words, it is a fraction divided by a fraction. Complex fractions contain variable expressions. To simplify, use the reciprocal of the divisor, then multiply.
Example
Simplify: \dfrac{\Big(\dfrac{\textit{x}}{\textit{y}}\Big)}{\Big(\dfrac{2\textit{x}}{3}\Big)}
Solution
Use the reciprocal then multiply.
\dfrac{\dfrac{\textit{x}}{\textit{y}}}{\dfrac{2\textit{x}}{3}} = \dfrac{\textit{x}}{\textit{y}} × \dfrac{3}{2\textit{x}} = \dfrac{3}{2\textit{y}}a https://www.youtube.com/watch?v=Cz-Gq4tqQ6c
a https://youtu.be/lJpIalg4gQo
a https://youtu.be/K8EstiKG1eM
a https://youtu.be/inJQglvyYSc
(need answer choices)
ahttps://youtu.be/K8EstiKG1eM (good for division)
a https://youtu.be/inJQglvyYSc (good for division)
a https://www.youtube.com/watch?v=22hmzJGpSJg
a https://www.youtube.com/watch?v=5QvUy25YuAs
Cross Multiplication
What is the best way to compare fractions?
Example
Which fraction is greater, \dfrac{3}{4} or \dfrac{8}{11}?
Solution
The LCD is 44, so compare
\dfrac{3}{4} = \dfrac{33}{44} and \dfrac{8}{11} = \dfrac{32}{44}.
So \dfrac{3}{4} is greater than \dfrac{8}{11},
or \dfrac{3}{4} > \dfrac{8}{11}.
An easier way to compare fractions is cross multiplication. Multiply the numerator of one fraction by the denominator of the other fraction and compare the products.
Example
Which fraction is greater, \dfrac{7}{30} or \dfrac{21}{91}?
Solution
Set the fractions next to each other and cross multiply.
\dfrac{\,\,7\,\,}{30} 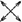 \dfrac{\,\,21\,\,}{91}
\dfrac{\,\,21\,\,}{91}
30 × 21 = 630
7 × 91 = 637
637 630 …Put the products under the corresponding numerator.
637 > 630, so \dfrac{7}{30} > \dfrac{21}{91}.
a https://www.youtube.com/watch?v=MkvXm1box58
a. https://www.youtube.com/watch?v=DMo7W9rE85Y
a. https://www.youtube.com/watch?v=Ncce2iWL6L8
a https://www.youtube.com/watch?v=5oEcfEHev34
a https://www.youtube.com/watch?v=jggipu2xfMU
Before attempting these problems, be sure to review this section on Quantitative Comparison questions.
https://www.youtube.com/watch?v=nH50bIl4G10&list=PLD0D070C218D8F5A3&index=1
https://www.youtube.com/watch?v=wjiFTuu3GnA&list=PLD0D070C218D8F5A3&index=7
https://www.youtube.com/watch?v=TYfcj6vtagc&list=PLD0D070C218D8F5A3&index=9
https://www.youtube.com/watch?v=RC4W_bWw-wY&list=PLD0D070C218D8F5A3&index=10
Video Quiz
Fractions
Best viewed in landscape mode
5 questions with video explanations
100 seconds per question
Are you sure you want to refresh the question?
Video Quiz
Fractions
Best viewed in landscape mode
4 questions with video explanations
100 seconds per question









