Geometry questions on the GRE are a logical puzzle. You will be given a tiny piece of information about a figure, and must deduce some piece of missing information. Geometry questions require you to follow a series of “if-then” statements, constantly solving the puzzle, piece by piece, in order to find the correct answer.
Lines
The most basic element in geometry is the point.
Through any two points, there is exactly one line, extending infinitely in both directions.
Lines can be named by two points or by a lower case letter.
A section of a line is called a line segment or a ray.

Angles
When two rays originate from the same point, they form an angle, which is represented by the symbol ∠.
The point of intersection is the vertex and the two rays form the sides of the angle.
An angle can be named in a number of ways.
It can be called ∠BAC where the middle letter is the vertex, ∠A where A is the vertex, or by a number inside the angle.

Angles are measured in degrees, denoted by the degree symbol °. For example, a 30 degree angle is written as 30°. A variable inside the angle, x°, stands for the measure of the angle.
Angles that have the same measure are congruent.
Congruent angles can be indicated with matching arcs. Congruent polygons can be indicated with the ≅ symbol.

Types of Angles
Angles can be categorized by their angle measure.

acute
0° < x° < 90°

right
90°
The box in the corner means that it is a right angle.

obtuse
90° < x° < 180°

straight
180°
A straight line is a 180° angle.
Two angles are complementary angles or complements if the sum of their measures is 90°.
Two angles are supplementary angles or supplements if the sum of their measures is 180°.
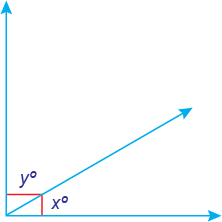
The sum x° + y° = 90°. These two angles are complementary angles.

The sum x° + z° = 180°. Notice that x° and z° create a straight line. These two angles are supplementary angles.
Example
In the figure, a beam of light is shown reflecting off a mirror. What is the value of x?

Solution
Because these three angles form a straight line, they must add up to 180°.
x + 3x + x = 180
5x = 180
x = 36
Example
The complement of an angle is one quarter of the supplement of the angle. What is the measure of the angle?
Section
Let x be the measure of the angle.
Its complement c is such that
x + c = 90, so x = 90 – c.
Its supplement s is such that
x + s = 180, so x = 180 – s.
The complement is one quarter of the supplement, so c = s/4.
90 – c = 180 – s …Subtract 90 and add s to both sides.
s – c = 90 …Substitute c = s/4.
s – s/4 = 90
3s/4 = 90 …Multiply both sides by 4/3.
s = 120
x + s = 180, so x = 180 – 120 = 60 so the measure of the angle is 60°.
Midpoint and Bisector
The midpoint is the center point of any line segment. In the figure below, point B is the midpoint of segment AC. The tick marks mean that the segments are the same length. They are congruent.

Example
In segment EH, F is the midpoint of segment EH, and G is the midpoint of segment FH. If EH = 8, how long is segment EG?

Solution
EH = 8, and the midpoint is F, so
FH = 4.
FH = 4, and the midpoint is G, so
GH = 2.
EF + FG = EG, so EG = 4 + 2 = 6.
Bisect means “to cut in half.” A bisector is a line that divides a line segment or an angle into two equal pieces.
Example
Ray TR bisects ∠STQ. What is the measure of ∠RTP?

Solution
∠STQ = ∠STR + ∠RTQ
∠STQ is a right angle, and since ∠STQ is bisected, ∠STR = ∠RTQ. So each angle is 45°.
The arcs show that ∠STR and ∠QTP are congruent.
So ∠STR = ∠QTP = ∠RTQ = 45°.
∠RTP = ∠RTQ + ∠QTP = 45° + 45°
= 90°
So the measure of ∠RTP is 90° and is right angle.
Another method is to notice that ∠STR + ∠RTQ = ∠RTQ + ∠QTP.
Since ∠STR = ∠QTP, ∠STQ = ∠RTP.
∠STQ is a right angle, so ∠RTP is also a right angle.






