Quantitative comparison questions do not require you to find an exact answer. Instead, these problems only require you to determine which of two values is greater, if the values are equal, or if there is not enough information to determine the relationship. Typically there are 7 or 8 quantitative comparison questions in each section.
Video Courtesy of Kaplan SAT prep.
Directions
Below are the directions for quantitative comparison questions. The directions are the same for all quantitative comparison questions, so once you become familiar with them you won’t need to waste time reading them on test day.
Directions: For each question, compare Quantity A and Quantity B, using additional information centered above the two quantities if such information is given. Select one of the following four answer choices.
Answer Choices
There are always the same four answer choices for quantitative comparison questions. Again, memorize the choices so you don’t waste time reading and understanding them on test day.
(A) Quantity A is greater.
(B) Quantity B is greater.
(C) The two quantities are equal.
(D) The relationship cannot be determined from the information given.
Question Format
Quantitative comparison questions will look like this. (The solution to the example is shown below.)
Example2x = y
Quantity A
The perimeter of an equilateral triangle, with side = yQuantity B
The perimeter of a square, with side = x(A) Quantity A is greater.
(B) Quantity B is greater.
(C) The two quantities are equal.
(D) The relationship cannot be determined from the information given.
Techniques
The Introduction contains a section about the seven techniques you can use to answer on SAT math questions.
Plug-In is the most common technique for quantitative comparison questions. Plug-In means you choose your own numbers to try in a question.
Remember these guidelines when using Plug-In.
- Make sure the numbers you choose fit the question’s parameters.
- Pick a variety of numbers to make sure you cover all reasonable possibilities.
- Try positive and negative numbers, and zero. For example, you could plug in -2, 0 and 2.
- If the question doesn’t specifically require “integers,” make sure to try some positive and negative fractions (a common trick on the SAT).
- Check all of the boundaries. For inequalities, if 0 ≤ x ≤ 3, try both 0 and 3. For other restrictions, such as even numbers, try the “boundary” value of 2.
The examples in this section show how to use Plug-In as well as other techniques.
Example2x = y
Quantity A
The perimeter of an equilateral triangle, with side = yQuantity B
The perimeter of a square, with side = x(A) Quantity A is greater.
(B) Quantity B is greater.
(C) The two quantities are equal.
(D) The relationship cannot be determined from the information given.
Solution
Calculate the perimeter of each polygon.
Perimeter of equilateral triangle = 3y
Perimeter of square = 4x
Use the equation to make both perimeters have the same variable. Substitute 2x for y.
Perimeter of equilateral triangle = 3y = 3(2x) = 6x
Since x and y are positive numbers, 6x > 4x. So quantity A is greater than quantity B.
The correct answer is (A).
Examplex < 0, y > 0
Quantity A
(x + y)2Quantity B
(x – y)2(A) Quantity A is greater.
(B) Quantity B is greater.
(C) The two quantities are equal.
(D) The relationship cannot be determined from the information given.
Solution
Method 1
This question is a good candidate for Plug-In. Choose values for x and y.
Let x = -2 and y = 2. Then
Quantity A: (x + y)2 = (-2 + 2)2 = 0
Quantity B: (x – y)2 = (-2 – 2)2 = (-4)2 = 16
For these values, quantity A is less than quantity B.
Choose values where | x | ≠ | y |. Let x = -1 and y = 4. Then
(x + y)2 = (-1 + 4)2 = (3)2 = 9
(x – y)2 = (-1 – 4)2 = (-5)2 = 25
For these values, quantity A is less than quantity B.
So quantity B is greater than quantity A.
The correct answer is (B).
Method 2
This question can also be solved quickly just using reasoning.
Use positive and negative with absolute value to represent squaring the values.
The value of (negative - positive) = (negative + negative)
| negative + positive | < | negative + negative |
So, | x + y | < | x – y |
Quantity B is greater than quantity A.
The correct answer is (B).
Examplea > b
Quantity A
a2Quantity B
b(A) Quantity A is greater.
(B) Quantity B is greater.
(C) The two quantities are equal.
(D) The relationship cannot be determined from the information given.
Solution
Quickly reading the question, it seems like a2 > b is always true. So there must be a trick. Plug-In is the best technique.
Try positive and negative numbers.
If a = 3 and b = 2, then 9 > 2.
If a and b are negative, then any a2 will be positive and greater than b.
The question doesn’t say “integers,” so try some positive fractions.
Let a = 1/2 and b = 1/3. Then a 2 = 1/4 and a2 < b.
Since a2 can be greater than or less than b, the answer is (D).
Notice that the question uses the variables a and b. This is another way the SAT checks your reasoning. Don’t confuse quantities A and B with variables or coordinate names, as in “segment AB.”
Examplex = 6, 9 ≤ y ≤ 10
Quantity A
x / yQuantity B
0.65(A) Quantity A is greater.
(B) Quantity B is greater.
(C) The two quantities are equal.
(D) The relationship cannot be determined from the information given.
Solution
This question is an inequality, so it’s a good candidate for Plug-In. Test the boundary values of y.
If y = 9, then x/y = 6/9 = 2/3 = 0.6.
If y = 10, then x/y = 6/10 = 0.6.
For the boundary values, quantity A can be less than or greater than quantity B.
There isn’t enough information to know which value is greater.
The correct answer is (D).
Examplex + 2y = 7
2x + y = 11Quantity A
x + yQuantity B
5(A) Quantity A is greater.
(B) Quantity B is greater.
(C) The two quantities are equal.
(D) The relationship cannot be determined from the information given.
Solution
This question looks like it requires solving a system of equations. But remember that the SAT is testing reasoning as much as math.
You are being asked the value of an expression, not x and y. This gives a hint you should solve for x + y.
Add the two equations.
x + 2y = 7
2x + y = 11
x + y = 6 Simplify.
For these values, quantity A is greater than quantity B.
The correct answer is (A).
ExampleQuantity A
16 – 82 ÷ 4 + 2 × 6Quantity B
(16 – 8)2 ÷ (4 + 2) × 6(A) Quantity A is greater.
(B) Quantity B is greater.
(C) The two quantities are equal.
(D) The relationship cannot be determined from the information given.
Solution
A common topic on the SAT is order of operations. The key is to only simplify far enough to be able to compare the values.
Quantity A: 16 – 82 ÷ 4 + 2 × 6 = 16 – 64 ÷ 4 + 12
Quantity B: (16 – 8)2 ÷ (4 + 2) × 6 = 82 ÷ 6 × 6
After simplifying each quantity by just one step, you can see that quantity A will be a smaller number than quantity B. So quantity B is greater than quantity A.
The correct answer is (B).
This would be a good question to mark. If you have enough time, you can return and finish simplifying the expressions to check your answer.
Quantity A: 16 – 82 ÷ 4 + 2 × 6 = 16 – 64 ÷ 4 + 12 = 16 – 16 + 12 = 12
Quantity B: (16 – 8)2 ÷ (4 + 2) × 6 = 82 ÷ 6 × 6 = 82 = 64
Absolute Value
Example| x + 2 | = 3x
Quantity A
xQuantity B
1(A) Quantity A is greater.
(B) Quantity B is greater.
(C) The two quantities are equal.
(D) The relationship cannot be determined from the information given.
Solution
Absolute value is a common topic on the SAT. Think and then simplify.
Since 3x is equal to an absolute value expression, 3x must be positive or 0. So x must be positive or 0.
Rewrite the equation without absolute value and solve.
x + 2 = 3x
2x = 2
x = 1
Quantity A is equal to quantity B.
The correct answer is (C).
Geometry
Video Courtesy of Kaplan GRE prep.
The directions for the SAT specifically say that any geometry figure may not be drawn to scale. Labeling the drawing with values or making a sketch that is to scale is important. Your sketch will help you see a ballpark answer.
Example
AB = BC
Quantity A
The area of triangle ABDQuantity B
The area of triangle CBD(A) Quantity A is greater.
(B) Quantity B is greater.
(C) The two quantities are equal.
(D) The relationship cannot be determined from the information given.
Solution
At first glance, there does not seem to be any way to solve this question.
Looking at the figure, the area of triangle ABD seems greater than area of triangle CBD.
The formula for the area of a triangle is: A = (1/2) bh
We are told AB = BC, so let those be the two bases.. You need to find the base and height of each triangle.
Draw a sketch of the figure with segment AC as the horizontal base.

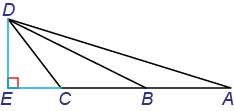
Now it is easy to see that the triangles have the same height.
Since the base and the height of each triangle is the same, the triangles have the same area.
The correct answer is (C).
Averages
The average (arithmetic mean) and median are often on the SAT. Using distances from the mean rather than calculating the mean can be the best technique.
ExampleThe set of data {10, 11, 17, 25, 32}
Quantity A
The arithmetic mean of the dataQuantity B
The median of the data(A) Quantity A is greater.
(B) Quantity B is greater.
(C) The two quantities are equal.
(D) The relationship cannot be determined from the information given.
Solution
This may seem like a question you should answer by plowing through the calculations. But first try a ballpark estimate by comparing the median and the mean.
The median is the middle number, 17.
The distances of 10 and 11 from the 17 are less than the distances of 25 and 32 from 17. (7 and 6 vs. 8 and 15)
For the data to “balance” at the mean, the mean will need to be closer to 25 and 32 than to 10 and 11. So the mean is greater than the median.
The correct answer is (A).
Calculating the mean by using the formula would take more time than using reasoning.
(10 + 11 +17 +25 +32) / 5 = 95/5 = 19
Since 19 > 17, the correct answer is (A).
ExampleThe average (arithmetic mean) of 70 test scores is 80. The average of 30 additional test scores is 90.
Quantity A
The average of the 100 test scoresQuantity B
85(A) Quantity A is greater.
(B) Quantity B is greater.
(C) The two quantities are equal.
(D) The relationship cannot be determined from the information given.
Solution
This may seem like a question you would answer by plowing through the calculations. But doing a quick calculation of the total differences can give a ballpark estimate.
Method 1
Find the difference for each batch of scores from the value in Quantity B, 85.
A score of 80 is 5 below 85, so the difference of all those tests scores from the average is 70(-5) = -350.
A score of 90 is 5 points above 85, so the difference of all those test scores from the average is 30(5) = 150.
The total of the differences from the averages and Quantity B is -350 + 150 = -200.
The negative means the average test score is lower than 85.
The correct answer is (B).
There are two methods to calculate the average rather than just estimation.
Method 2
One way is to continue with the total difference from the average.
The difference from the average score and 85 is -200 points/100 tests = -2. So the average of the 100 test scores is 2 less than 85, or 83.
The correct answer is (B).
Method 3
Using the formula, the average score would be
[70(80) + 30(90)] / 100 = (5600 + 2700) / 100 = 8300 / 100 = 83
Since 83 < 85, the correct answer is (B).
Other Problem Types
ExampleFor y > 0, let y* = 1 / y.
Quantity A
15*/3*Quantity B
(15/3)*(A) Quantity A is greater.
(B) Quantity B is greater.
(C) The two quantities are equal.
(D) The relationship cannot be determined from the information given.
Solution
Occasionally there are functions using strange symbols on the SAT. Since the quantities in this example have numbers, simplify each quantity.
Quantity A
15* / 3* = (1/15) / (1/3) = (1 /15) × (3 / 1) = 1/5
Quantity B
(15/3)* = 1/(15/3) = 3/15 = 1/5
Quantity A is equal to quantity B.
The correct answer is (C).
ExampleA pizza parlor offers 6 different toppings on thick or thin crust.
Quantity A
The number of different 2-topping pizzasQuantity B
15(A) Quantity A is greater.
(B) Quantity B is greater.
(C) The two quantities are equal.
(D) The relationship cannot be determined from the information given.
Solution
Use the formula for combinations.
n C r = \dfrac{\textit{n}!}{\textit{r}! (\textit{n} \,-\, \textit{r})!}
with n distinct objects to choose from and r objects chosen.
For the toppings, there are 6 options and we are selecting 2.
6 C 2 = 6! / 2!(6 – 2)! = 6! / 2! × 4! = 6 × 5 × 4! / 2! × 1 × 4! = 30 / 2 = 15
But don’t stop there. This is a SAT trick. Quantity B is the value before you actually complete the calculations. It is the number of topping combinations, not the total number of different pizzas.
Since there are 2 types of crust, the total number of different pizzas is 15 × 2 = 30.
Quantity A is greater than quantity B.
The correct answer is (A).








