Definitions
An inequality compares two quantities or expressions. There are four inequality symbols: <, ≤, >, and ≥.
a < b
a is less than b.

x < 2
a ≤ b
a is less than or equal to b.

x ≤ 2
a > b
a is greater than b

x > -1
a ≥ b
a is greater than or equal to b.

x ≥ -1
An easy way to remember which way the symbol should open is to use “the crocodile eats the larger number.”
5 > 3 is equivalent to 3 < 5. y ≤ 7 is equivalent to 7 ≥ y.
A compound inequality is two separate inequalities that show a range of values.
x > -2 and x ≤ 3

y ≤ 0 or y > 4
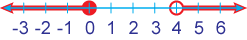
Combine these inequalities to show the range of values:
8 ≥ x, x > -4 and x – 3 < 3
Solution
x – 3 < 3
x – 3 + 3 < 3 + 3
x < 6
Rewrite the inequalities so the symbols all point to the left. (Make sure “the crocodile still eats the larger number.”)
Align the variables.
xxxxx < 8
-4 < x
xxxxx < 6
The range for x must satisfy the most limited values of the inequalities. For the lower boundary, -4 is in all three inequalities. For the upper boundary, 6 is in all three inequalities.
The range for x is between -4 and 6. -4 < x < 6
Another way to check a range of values is with a sketch. The overlap of all of the inequalities is the range.
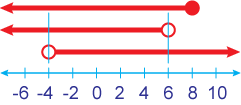
Range, Minimum and Maximum
If 2 ≤ x ≤ 5 and y > 6, what is the range of values for xy?
Solution
Compare the minimum values and multiply.
The minimum value for x is 2 and the minimum for y is 6, so the minimum for xy is 12.
Compare the maximum values and multiply.
The maximum value for x is 5 and y has no maximum, so xy has no maximum. The range is xy > 12.
If -3 ≤ x ≤ 3 and y < 6, what is the range of values for xy?
Solution
Compare the minimum values and multiply.
The minimum value for x is -3 and y has no minimum, so xy has no minimum.
Compare the maximum values and multiply.
The maximum value for x is 3 and the maximum value of y is 6, so it looks like the maximum of xy is 18. But since x and y can both be negative numbers and y has no lower limit, xy can be a large positive or negative number.
For example,
if x = -3 and y = -1,000,
then xy = 3,000.
If x = 3 and y = -1,000,
then xy = -3,000. So xy can be any number.
Absolute Value
Absolute value is another way to express a range of values. The absolute value equation | x | = 2 means the distance between x and 0 is 2. There are two solutions, 2 and -2.
The absolute value inequality | x | < 2 means the distance between x and 0 is less than 2, so x > -2 and x < 2.

The inequality | x | ≥ 2 means the distance between x and 0 is greater than or equal to 2, so x ≤ -2 or x ≥ 2.
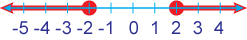
Video Quiz
Inequalities
Best viewed in landscape mode
5 questions with video explanations
100 seconds per question
Are you sure you want to refresh the question?
https://www.youtube.com/watch?v=F0PDA1jXVmE
https://www.youtube.com/watch?v=MrrR6wo4TxI
https://www.youtube.com/watch?v=Jd6QMrqoXKA (absolute value)
https://www.youtube.com/watch?v=XIQm52Csj9k (absolute value)
https://www.youtube.com/watch?v=78kcmq6kYPQ (absolute value)
Before attempting this problem, be sure to review this section on data sufficiency questions.
https://www.youtube.com/watch?v=rt26153cBQQ (absolute value)
The absolute value of a number, written as | -5 |, is the distance of a number from zero on the number line: | +5 | = | -5 | = 5.
The value of an expression inside the absolute value signs could be positive or negative.
If | x | = 7, then x could be 7 or -7.
This means that absolute value equations usually have two possible solutions.
| x + 3 | = 8.
Solution
x + 3 = 8 or x + 3 = -8 …Rewrite as two equations.
x = 5 or x = -11 …Two solutions.
| -2x2 | – (\dfrac{3\textit{x}}{2})2 × 2
Solution
| -2x2 | – (\dfrac{3\textit{x}}{2})2 × 2
2x2 – \dfrac{9\textit{x}^{\displaystyle{2}}}{4} × 2 …Do operations inside grouping symbols: absolute value and parentheses.
2x2 – \dfrac{9\textit{x}^{\displaystyle{2}}}{2} …Multiply.
\dfrac{4\textit{x}^{\displaystyle{2}}}{2} \,-\, \dfrac{9\textit{x}^{\displaystyle{2}}}{2} …Use the common denominator and subtract.
\dfrac{-5\textit{x}^{\displaystyle{2}}}{2}Solving Inequalities
Solving an inequality uses many of the same rules as solving an equation.
- The same number or algebraic expression may be added or subtracted from both sides of an inequality.
- The same positive number may multiply or divide both sides of an inequality.
Solving Inequalities
There is one rule for solving inequalities that is different than the rule for solving equations:
- If a negative number multiplies or divides both sides of an inequality, the inequality sign must be “reversed.”
This is the most common mistake when solving inequalities.
Look at 4 > 3. Multiply both sides by -1. The values become -4 ? -3.
Since -4 is less than -3, the sign reverses and the inequality is -4 < -3.
An additional note about this rule: You can only divide or multiply by a variable or expression if you know the sign (positive or negative) of the variable or expression. This topic will be covered later in this chapter.
-6(2y – 2) > 15
Solution
-6(2y – 2) > 15 …Use the distributive property.
-12y + 12 > 15 …Subtract 12 from both sides.
-12y > 3 …Divide both sides by -12.
y < \dfrac{-1}{4} …Make sure to reverse the inequality sign.
Solving Systems of Inequalities
Inequalities can be added if both inequality symbols point the same way. You can multiply one of the inequalities by -1 so the symbols match. Always add, not subtract, inequalities.
When solving systems of equations or inequalities, you solve for a single variable: y = 3 or z > 2.
In solving a system of equations, you would substitute that value into either of the original equations.
Video Courtesy of Kaplan GMAT prep.
y – 2x > 0 and 3x – y > 0
Solution
y – 2x > 0 …Add the inequalities.
3x – y > 0
x > 0
y – 2x > 0 …Add the new inequality to one of the original inequalities.
x > 0
y – x > 0 …Add x to both sides.
x > 0 and y > x
4x + 3y > 0 and 3x + 3y < 0
Simplify:
3x + 3y < 0 …Multiply by -1 so the inequality symbols of the inequalities match.
–3x – 3y > 0
4x + 3y > 0 …Add the inequalities.
-3x – 3y > 0
x > 0
3x + 3y < 0 …Divide by 3.
x + y < 0
–x < 0 …Multiply (x > 0) by -1. Then add the inequalities.
x + y < 0
x > 0
x > 0 and y < 0
You can take this solution one step further.
Since x + y < 0, subtract y from both sides. Then x < –y.
So x > 0, y < 0 and x < –y.
Using Substitution
Substituting values into an inequality can often be helpful.
Let x2 – 4 > 0 for the integer x. Which of the following represents the range of x?
(A) x > -2
(B) x < 2
(C) -2 < x < 2
(D) x > 2 or x < -2
(E) 1 > x > -2
Solution
If there was an equality sign, the solutions for x2 – 4 = 0 would be -2 and 2. But with an inequality sign, 2 and -2 define the boundaries of the inequality x2 – 4 > 0.
Substitute x = 0 into the inequality.
02 – 4 is not greater than 0, so the inequality does not include 0.
Only answer choice (D) does not include 0, so it is correct.
The integers x, y, z are all less than 30, and x + y + z > 67. Of the three integers, how many are postive?
Simplify:
All three numbers must be less than 30. Try x = y = 29 so two of the numbers are as large as possible.
x + y + z = 29 + 29 + z = 58 + z. So for x + y + z > 67, z must be positive. Therefore, all three integers must be positive.
For any of the numbers to be negative, at least one would have to be greater than 30.
Inequalities in Triangles
There is one inequality in triangles that is often used on the GMAT.
The sum of the lengths of any two sides of a triangle must be greater than the length of the third side.
The lengths of two sides of a triangle are 4 inches and 7 inches. What is the range of possible lengths of the third side?
Solution
The sum of the two sides is 4 + 7 = 11. The longest the side must be less than 11 inches or the triangle would just be a line.
The difference in lengths of the two sides is 7 – 4 = 3. The shortest side must be longer than 3 inches or the sides would be too short to connect.
The range is 3 < x < 11.
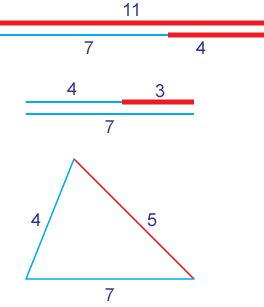
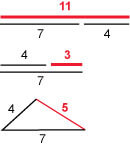
The lengths of the sides of a triangle are x, x + 2, and x + 4. If x is an integer, what is the range of possible values of x?
Solution
Add 4 to all three terms.The sum of the lengths of the two shortest sides needs to be greater than the longest side.
x + (x + 2) > x + 4
Subtract x + 2 from both sides,
and x > 2.
Since x is an integer and x > 2, the range is x ≥ 3.
Substitution (plugging in values) is an alternate way to find possible values.
| x | x + 2 | x + 4 | |||
| 1 | 1 | 3 | 5 | 1 + 3 < 5: not a triangle |
|
| 2 | 2 | 4 | 6 | 2 + 4 = 6: not a triangle |
|
| 3 | 3 | 5 | 7 | 3 + 5 > 7 and 7 – 5 < 3: triangle |
Since x = 3 works, x ≥ 3. |
| 4 | 4 | 6 | 8 | 4 + 6 > 8 and 8 – 6 < 4: triangle |
You can check by substituting one more value of x. |
Video Quiz
Inequalities
Best viewed in landscape mode
6 questions with video explanations
100 seconds per question
Are you sure you want to refresh the question?
https://www.youtube.com/watch?v=yVKy7uVlVXc
https://www.youtube.com/watch?v=85KoA3PjzSY
https://www.youtube.com/watch?v=b9R_688CRJ8
https://www.youtube.com/watch?v=iRCggo2AEvQ
https://www.youtube.com/watch?v=DdKyqeVBb68
https://www.youtube.com/watch?v=cRUYvxNSBOY
https://www.youtube.com/watch?v=5FyW40hCQl4 (inequalities)
Before attempting these problems, be sure to review this section on data sufficiency questions.
https://www.youtube.com/watch?v=1VAEquQ71xA
https://www.youtube.com/watch?v=oJ61mSE40PM
https://www.youtube.com/watch?v=DewYx-7NTtA
https://www.youtube.com/watch?v=i1hGEeBOLnY
https://www.youtube.com/watch?v=vAGdG7pc6lY
https://www.youtube.com/watch?v=7olME16D4MY
https://www.youtube.com/watch?v=_mMhQNrbrCM
https://www.youtube.com/watch?v=1NYh8nV8W54
https://www.youtube.com/watch?v=klMRTdPM9K0
https://www.youtube.com/watch?v=9j0jBSc8KlE
https://www.youtube.com/watch?v=YdO5GFMBcKQ (inequalities)








