Types of Polygons
A polygon is a figure made from 3 or more line segments. The segments, called sides, intersect at the endpoints of the segments, called vertices (singular: vertex). Congruent polygons can be indicated with the ≅ symbol.
There are many types of polygons.
| quadrilateral | 4 sides |
| pentagon | 5 sides |
| hexagon | 6 sides |
| octagon | 8 sides |
| n-gon | polygon with n sides |
| equilateral | all sides equal |
| equiangular | all angles equal |
| regular | all sides equal and all angles equal |
| convex | all angles point “out” |
| concave | has an angle that points “in” |
Triangles and quadrilaterals are the most common polygons on the GMAT. Other polygons on the test usually contain triangles and quadrilaterals.
Parallelograms
Video Courtesy of Kaplan GMAT prep.
Perimeter and Area
The perimeter of a polygon is the distance around the outside of the polygon, or the sum of the lengths of the sides of the polygon.
The area of a polygon is the amount of surface that is covered by the polygon.
To find the area of triangles and quadrilaterals, you need two measurements: the base and the height.
Any of the sides of a triangle can be its base. The height of the triangle is the perpendicular distance from the base to the opposite angle.
For the quadrilaterals listed below, the height of the quadrilateral is the perpendicular distance from the base to the opposite side.
These are the formulas for the perimeter, P, and area, A, of common figures.
Triangle

P = a + b + c
A = \dfrac{1}{2} (base × height) = \dfrac{1}{2}bh
Right Triangle

P = leg + leg + hypotenuse
A = \dfrac{1}{2} (leg × leg) = \dfrac{1}{2}bh
Rectangle

P = 2l + 2w = 2(l + w)
A = length × width = lw
or
A = base × height = bh
Opposite sides are equal.
All angles are equal and are 90°
Square

P = 4s
A = s2
All sides are equal.
All angles are equal and are 90°.
Parallelogram
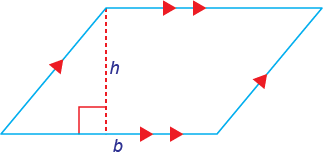
P = 2l + 2w = 2(l + w)
A = base × height = bh
Opposite sides are equal.
Opposite sides are parallel.
Opposite angles are equal.
Adjacent angles add to 180°.
Rhombus
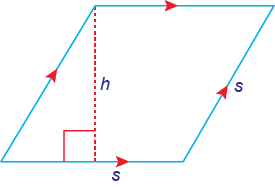
P = 4s
A = base × height = bh
All sides are equal.
Opposite sides are parallel.
Opposite angles are equal.
Adjacent angles add to 180°.
Trapezoid

P = a + b1 + c + b2
A = \dfrac{1}{2}(base 1 + base 2)(height)
= \dfrac{1}{2}(b1 + b2)h
One pair of opposite sides, the bases, is parallel.
Circle

C = 2πr = πd
A = πr2
r = radius, d = diameter, and d = 2r
π ≈ 3.14 ≈ \dfrac{22}{7}
Note: A circle is not a polygon. Circles are covered in the next section.
Find the perimeter and area of the figure.
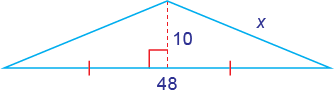
Solution
The area of the triangle is
A = (\dfrac{1}{2})(48)(10) = 240 square units
To find the perimeter, use the right triangle formed by the height and half of the base.
That triangle’s side lengths are
10 : 24 : x.
This is a multiple of a
5 : 12 : 13 triangle, so x = 2(13) = 26.
P = 48 + 26 + 26 = 100 units
Find the area of the shaded region.

Solution
The shaded region is a rectangle minus a trapezoid.
The area of the rectangle is
A = (8)(5) = 40 square inches.
The side lengths of the trapezoid are height = 2, base1 = 3 and base2 = 5.
A = (\dfrac{1}{2})(3 + 5)(2) = 8 square inches.
The area of the shaded region is
40 – 8 = 32 square inches.
Video Quiz
Polygons
Best viewed in landscape mode
5 questions with video explanations
100 seconds per question
Are you sure you want to refresh the question?
Interior and Exterior Angles
The sum of the interior angles of a polygon is a function of the number of sides. The formula for the sum of the interior angles of a polygon with n sides is (n – 2)180°.
For a triangle, the sum of the interior angles is 180°.
A quadrilateral has 4 sides, so n = 4.
The sum of the interior angles of a quadrilateral is
(4 – 2)180° = 2(180°) = 360°.
For a hexagon, n = 6 so the sum of the interior angles is
(6 – 2)180° = 4(180°) = 720°.

For a triangle, the sum of the interior angles is 180°.
If you can’t remember the formula for the sum of the interior angles, count the number of the triangles formed when all the diagonals are drawn from just one vertex. The sum of interior angles is the number of these triangles times 180°. (See more about diagonals below.)
The sum of the exterior angles of all polygons is 360°.
You can think of this as going all the way around the polygon, making a complete circle.

What is the measure of the smallest interior angle of the polygon?

Solution
The polygon has 5 sides, so the sum of the interior angles is
(5 – 2)(180°) = 540°.
Find the value of x.
95 + 70 + x + 2x + 2x = 540
5x = 540 – (95 + 70) = 375
x = 75
Be careful to remember the question is not asking for x, but for the smallest interior angle. Because x = 75, the smallest interior angle is 70°.
Find the measures of all of the angles.
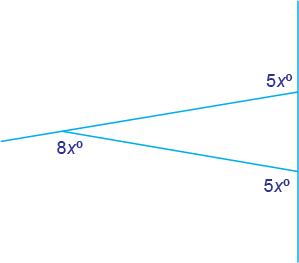
Solution
The sum of the exterior angles is 360°, so
5x + 8x + 5x = 360
18x = 360
x = 20
The exterior angle measures are 100°, 100° and 160°.
The interior and exterior angles are supplementary so each pair adds to 180°.
180 – 100 = 80 and 180 – 160 = 20
The measures of the interior angles are 80°, 80° and 20°.
Symmetry
A figure has line symmetry if the figure can evenly “fold” onto itself. A figure can have more than one line of symmetry.
A figure has rotational symmetry if the figure can be rotated less than 180° and lines up on the original figure.
The point used for the rotation is the center of symmetry.
Identify the line symmetry and rotational symmetry of the figures.

Solution
The isosceles trapezoid has 1 line of symmetry. It has no rotational symmetry.

Identify the line symmetry and rotational symmetry of the figures.

Solution
The equilateral triangle has 3 lines of symmetry.
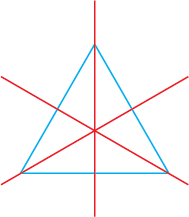
Rotating the triangle 120° and -120° matches the original triangle.

Similar Polygons
Polygons that have the same shape but a different size are called similar polygons.
Polygons are similar if the corresponding angles are equal, and the corresponding sides have the same ratio.
The ratio of the lengths of the corresponding sides is called the scale factor. The scale factor for congruent figures is 1.
Some polygons are similar by definition. For example, all equilateral triangles are similar, all squares are similar, and all circles are similar.
A line parallel to the base of a triangle or a trapezoid also creates similar polygons.
Segment AB is parallel to segment CD. Find the values of the variables.

Solution
Since AB is parallel to CD, triangles AEB and CED are similar.
The top small triangle CED is a right triangle. The side lengths are
8 : x : 17, so x = 15.
Compare 15 and 7.5 to find the ratio: 7.5 is what fraction of 15? Since 7.5 is half of 15, y will be half of 8. So y = 4.
The side AB will not be half of side CD. If you compare triangles AEB and CED, AEB is one and a half (1.5) times as big as CED.
Since AB will be 1.5 times CD,
z = 1.5(17) = 25.5.
The trapezoids ABCD and SPEN are similar. Segment AB is parallel to segment CD. Segment NE is parallel to segment SP. Find the angle measures and the perimeter of both trapezoids

Solution
Since AB is parallel to DC,
∠C + ∠B = 180°, so ∠B = 90°.
∠N + ∠S = 180°, so ∠S = 180° – 65°
= 115°.
Since NE is parallel to SP,
∠N + ∠S = 180°, so ∠S = 180° – 65°
= 115°.
Use the correspondence between the angles in ABCD and SPEN.
The angle measures are
∠C = ∠E = 90°
∠B = ∠P = 90°
∠A = ∠S = 115°
∠D = ∠N = 65°
The longest side in ABCD is 12. The longest side in SPEN is 30. Find the scale factor.
\dfrac{\textit{ABCD}}{\textit{SPEN}} = \dfrac{12}{30} = \dfrac{2}{5}
\\[3ex]\dfrac{\textit{AB}}{\textit{SP}} = \dfrac{3}{\textit{x}} = \dfrac{2}{5}. SP = 15/2 = 7.5
\dfrac{\textit{BC}}{\textit{PE}} = \dfrac{11}{\textit{y}} = \dfrac{2}{5}. PE = 55/2 = 27.5
The perimeter of SPEN is
30 + 7.5 + 27.5 + 20 = 85.
Instead of calculating CD, use the scale factor to find the perimeter of ABCD.
The perimeter of ABCD is
(2/5)(85) = 34.
Diagonals
A diagonal of a polygon is a segment that connects two non-adjacent vertices of the polygon.
Diagonals of a polygon form triangles inside the polygon.
The GMAT often uses the triangles formed inside quadrilaterals by the diagonals. The more you know about the quadrilateral, the more you know about the diagonals and the triangles that are formed. Drawing sketches can help you remember common diagonals. Two sketches are drawn for you below.
parallelogram
One diagonal of a parallelogram divides the parallelogram into two congruent triangles.
The diagonals of a parallelogram bisect each other.
rectangle
One diagonal of a rectangle divides the rectangle into two congruent triangles.
The diagonals of a rectangle are equal and bisect each other.
rhombus
One diagonal of a rhombus divides the rhombus into two pairs of two congruent triangles.
Two diagonals of a rhombus divide the rhombus into four congruent triangles.
The diagonals of a rhombus are perpendicular and bisect each other.
The diagonals of a rhombus bisect the angles of the rhombus.
∠ABC ≅ ∠ADC ∠BAD ≅ ∠BCD
∠1 = ∠2 = ∠3 = ∠4
∠5 = ∠6 = ∠7 = ∠8
AE = EC BE = ED
∠BEA = ∠BEC = ∠DEA = ∠DEC = 90°
triangles BEA ≅ BEC ≅ DEA ≅ DEC
triangles BDC ≅ BDA
triangles BAC ≅ DCA

square
One diagonal of a square divides the square into two 45° : 45° : 90° triangles.
The diagonals of a square are equal, perpendicular and bisect each other.
The diagonals of a square bisect the angles of the square.
isosceles trapezoid
The diagonals of an isosceles trapezoid are equal.
The diagonals of an isosceles trapezoid divide the trapezoid into two congruent triangles.
Given trapezoid with AB = CD
AC = BD
triangles ABD ≅ DCA

Maximum and Minimum
The GMAT often asks for the maximum or minimum perimeter or area. Maximum area is when a triangle or quadrilateral has perpendicular sides and right angles.
Squares and 45° : 45° : 90° triangles have the maximum area for the smallest perimeter.
Find the maximum area of a quadrilateral with perimeter 40 feet.
Solution
A square is the type of quadrilateral that has the maximum area.
If the perimeter of the square is 40 feet, the length of each side is 10 feet. The area is 102 = 100 square feet.
Find the minimum perimeter of a quadrilateral with an area of 16 square meters.
Solution
Use the method of plugging in values for the sides of different quadrilaterals that have an area of 16.

The square has the smallest perimeter for the given area.
The minimum perimeter is 16 meters.
Find the maximum area of a triangle where one side is 5 inches and the other side is 9 inches.
Solution
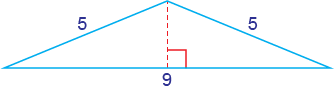
This isosceles triangle has sides of 5, 5 and 9.
Using the Pythagorean theorem, the height is about 2.
A ≈ (1/2)(9)(2) ≈ 9 in.2

Part of this triangle is a 3 : 4 : 5 right triangle, so the height of the triangle is 3.
A = (1/2)(9)(3) = 13.5 in.2

This right triangle has 5 and 9 as the legs.
A = (1/2)(9)(5) = 22.5 in.2
The maximum area is 22.5 square inches.
Video Quiz
Polygons
Best viewed in landscape mode
3 questions with video explanations
100 seconds per question
Are you sure you want to refresh the question?
https://www.youtube.com/watch?v=XOX4Vsaxt4s
https://www.youtube.com/watch?v=nsb4Ngj0e7U
Before attempting these problems, be sure to review this section on data sufficiency questions.
https://www.youtube.com/watch?v=YsB8qB3eG98
https://www.youtube.com/watch?v=kb76gnDaEIc







