Rectangular Prisms
A rectangular prism, or rectangular solid, is basically a box.
It has 6 sides.
All the sides, or faces, are rectangles. Opposite sides are congruent.

A good way to visualize a solid is to “unfold” the box and look at the net.
It is easy to see the 6 rectangles, and that opposite sides are equal.
The surface area, SA, is the sum of the areas of each pair of congruent sides.
SA = 2lh + 2lw + 2hw = 2(lh + lw + hw)

To find the volume of a rectangular prism, multiply the three lengths.
V = length × width × height = lwh
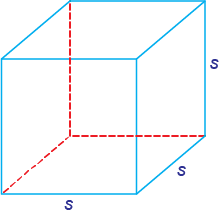
A special rectangular prism is a cube.
All the faces are squares.
If the length of a side is s, then:
SA = 6 × area of one side = 6s2
V = s3
Finding area and volume often uses multiplication of polynomials.
The dimensions of a box are
(y + 2) feet long, (y + 7) feet wide and (2y – 4) feet high. What is the area of the bottom of the box?
Solution
To find the area of the bottom of the container, multiply length by width, which are the first two binomials.
(y + 2)(y + 7)
= y(y + 7) + 2(y + 7)
= y2 + 9y + 14
The dimensions of a box are
(y + 2) feet long, (y + 7) feet wide and (2y – 4) feet high. What is the volume of the box?
Solution
To find the volume, multiply the area of the bottom by the height.
(2y – 4)(y2 + 9y + 14)
= (2y3 + 18y2 + 28y)
– (4y2 + 36y + 56)
= 2y3 + 14y2 – 8y – 56
Cylinders
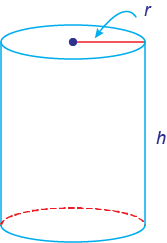
A cylinder is like a can. It has circles as the top and base, and straight sides.
A good way to visualize a cylinder is to “unwrap” it and look at the net.
The two circles are easy to see.
The body of the cylinder is a rectangle.
One side of the rectangle is the height of the can.
The other side of the rectangle is wrapped around the circles, so is the circumference of the circle.

SA = 2 circles + rectangle = 2(πr2) + 2πrh
To find the volume of a cylinder, multiply the area of the base by the height:
V = πr2h
It takes about 7.5 gallons to fill a volume of one cubic foot. How many gallons are needed to fill a cylinder 2 feet high with a radius of 28 inches?
Solution
Notice that the volume is given in feet but the lengths are given in feet and inches. Change inches to feet before calculating.
\dfrac{inches}{12} = 1 foot
\dfrac{28 \,inches}{12\, inches} = \dfrac{7}{3} feet
Calculate the volume of the cylinder.
V = πr2h = π (\dfrac{7}{3})2(2) Use \dfrac{22}{7} for π.
= (\,\dfrac{\,22\,}{7}\,)(\,\dfrac{\,49\,}{9}\,)(2) = \dfrac{22 × 7 × 2}{9}
= \dfrac{44 × 7}{9} = \dfrac{308}{9}
The volume of a cylinder is \dfrac{308}{9} cubic feet.
Since it takes 7.5 gallons to fill one cubic foot, multiply the volume by 7.5.
\dfrac{308}{9} × 7.5 = \dfrac{308 × 3 × 2.5}{9}
= \dfrac{308 × 2.5}{3} = \dfrac{616 + 154}{3}
= \dfrac{770}{3} = 256 \,\dfrac{2}{3}
The cylinder can hold 256 \dfrac{2}{3} gallons.
A gallon of paint covers 400 square feet of wall. How many gallons are required to paint the walls of a building with perimeter 200 feet and height 10 feet that has no windows?
Solution
The area to be painted is just the walls, not the top or bottom.
The perimeter is the distance around the building, that is, the length of the rectangles that make up its sides. The length of each rectangle isn’t needed, only the sum of the lengths.
![]()
Each rectangular side is 10 feet high, so the area is:
A = bh = 200 × 10 = 2,000 ft2
Divide the square feet by 400 ft/gal.
Number of gallons required
= \dfrac{2.000}{400} = 5 gallons
Note: The shape of the building makes no difference here. The building could be a cylinder. The perimeter would be the circumference of the base and top.
Spheres
A sphere is like a ball. The formulas for circumference, surface and volume all use the radius.

The circumference is the same as a circle.
C = 2πr = πd
Surface area
SA = 4πr2
Volume
V = (\dfrac{4}{3}) πr3
A can of tennis balls contains 3 stacked tennis balls. The tennis balls touch the sides, top and bottom of the container. If the circumference of a tennis ball is 8 inches, approximately how much space in the container is not taken up by the tennis balls?
(A) 6 in.3
(B) 13 in.3
(C) 17 in.3
(D) 19 in.3
(E) 26 in.3
Solution
Use the circumference of a tennis ball to find the radius of the balls and the container.
C = 2πr
8 = 2πr
r = (\dfrac{4}{\textit{π}})

The volume of one tennis ball is
V = \dfrac{4}{3} πr3 = \dfrac{4}{3} π (\dfrac{4}{\textit{π}} )3
= \dfrac{4 × \textit{π} × 4^{\displaystyle{3}}}{3 × {\textit{π}}^{\displaystyle{3}}} = \dfrac{4^{\displaystyle{4}}}{3{\textit{π}}^{\displaystyle{2}}}
The volume of 3 tennis balls will be:
3(\dfrac{4^{\displaystyle{4}}}{3{\textit{π}}^{\displaystyle{2}}}) = \dfrac{4^{\displaystyle{4}}}{{\textit{π}}^{\displaystyle{2}}}
The height of the cylindrical can is as tall as 3 balls, and the height of one ball is its diameter, which is 2(\dfrac{4}{π}).
The volume of the can minus the ball is
\dfrac{3 × 2 × 4^{\displaystyle{3}}}{{\textit{π}}^{\displaystyle{2}}} \,-\, \dfrac{4^{\displaystyle{4}}}{{\textit{π}}^{\displaystyle{2}}}
= \dfrac{4^{\displaystyle{3}}(6 \,-\, 4)}{{\textit{π}}^{\displaystyle{2}}} …Factor out the common factor, 43.
= \dfrac{4^{\displaystyle{3}}(2)}{{\textit{π}}^{\displaystyle{2}}} = \dfrac{64 × 2}{{\textit{π}}^{\displaystyle{2}}} = \dfrac{128}{{\textit{π}}^{\displaystyle{2}}}
Use estimates of π2 = 9 and π2 = 10, and get values between 14.2 and 12.8.
The closest answer choice is (B).
Video Quiz
Solids
Best viewed in landscape mode
3 questions with video explanations
100 seconds per question
Are you sure you want to refresh the question?
https://www.youtube.com/watch?v=uoiFHPUkhEw
https://www.youtube.com/watch?v=i-Bl4zJmw-Q
Before attempting this problem, be sure to review this section on data sufficiency questions.







